تمرین

پاسخ:

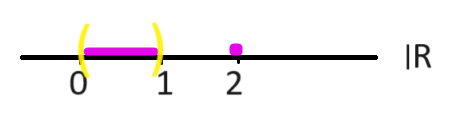
- A° = (0,1)

- Ext(A) = (-∞,0) ∪ (1,2) ∪ (2,∞)

- {0,1,2} = (A)∂

- [0,1] ∪ {2} = \(\overline{A} \)

و بنابراین A° = (0,1) ≠ [0,1] = Ā.

پاسخ:

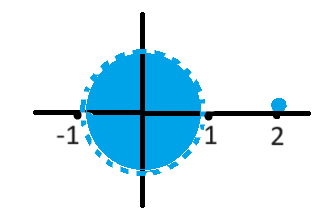
- A° = {(x,y) | x²+y² < 1}

- Ext(A) = {(x,y) | x²+y² > 1, (x,y) ≠ (2,0)}

- {(x,y) | x²+y² = 1} ∪ {(2,0)} = (A)∂

- Ā = {(x,y) | x²+y² ≤ 1} ∪ {(2,0)}

پاسخ:

- با متریک اقلیدسی: A° = ∅ ، ∂A = A ، Ā = A.

- با متریک گسسته: A° = A ، ∂A = ∅ ، Ā = A.

پاسخ:

-الف) A° = ∅ تعریف: x∈ A اگر یک بازه باز ( 𝑥 − 𝑟 , 𝑥 + 𝑟 ) وجود داشته باشد که کاملاً در A قرار گیرد.

اما A=Q∩[0,1] است، یعنی اعداد گویا بین 0 و 1. در هر بازه باز ( 𝑥 − 𝑟 , 𝑥 + 𝑟 ) هم عدد گویا وجود دارد و هم عدد غیرگویا.

بنابراین هیچ بازه‌ای را نمی‌توان پیدا کرد که کاملاً داخل A باشد. ⇒int(A)=∅

- Ā = [0,1] تعریف: یک مجموعه بسته است اگر مکمل آن باز باشد.

در هر بازه (x−r,x+r)⊂[0,1] اعداد گویای بی‌شماری وجود دارد (زیرا اعداد گویا در R متراکم‌اند).

بنابراین تمام نقاط x∈[0,1] در بستار A هستند: Ā = [ 0 , 1 ]

- ب) [0,1]= A∂

تعریف: Ā - A° = A∂

از قسمت (الف) می‌دانیم که A° = ∅ و Ā = [0,1] . بنابراین:

∂A = Ā - A° = [0,1] - ∅ = [0,1]

- ج) °(A∂) ≠ ∅.

از قسمت (ب) می‌دانیم که [0,1]= A∂ .

درون [0,1] برابر با (0,1) است که تهی نیست.

int(∂A)=(0,1) ≠ ∅

بنابراین مجموعه A=Q∩[0,1] خودش مثال مناسبی است.

پاسخ تمرین 6

- الف) °A = ∅ و Ā = A.

تعریف: x∈ A اگر یک بازه باز (x−r,x+r) وجود داشته باشد که کاملاً در A قرار گیرد.

اما A={1/n | n ∈ ℕ} ∪ {0} است، یعنی مجموعه‌ای از نقاط ایزوله که به 0 همگرا می‌شوند. در هر بازه باز (x−r,x+r) که شامل یک نقطه از A باشد، نقاطی خارج از A نیز وجود دارد.

بنابراین هیچ بازه‌ای را نمی‌توان پیدا کرد که کاملاً داخل A باشد. ⇒°A = ∅

برای Ā = A:

تعریف: یک مجموعه بسته است اگر مکمل آن باز باشد.

از آنجایی که تمام نقاط A شامل نقاط تجمع خود هستند (به ویژه 0)، هیچ نقطه‌ای خارج از A وجود ندارد که به A نزدیک شود. بنابراین، Ā = A.

- ب)A = ∂A.

تعریف: Ā - °A = ∂A

از قسمت (الف) می‌دانیم که °A = ∅ و Ā = A . بنابراین:

A = A - ∅ = Ā - A° = ∂A