نقاط درونی، بیرونی و مرزی و بستار یک مجموعه
مقدمه
در این صفحه، به مفاهیم مهمی مانند فضاهای متریک، همسایگی، نقاط درونی، بیرونی، مرزی و بستار یک مجموعه میپردازیم. این مفاهیم در توپولوژی و تحلیل ویژه نقش حیاتی دارند.
هدف فراهم اوردن این بستر برای آموزش نقاط درونی ، بیرونی ، مرزی و بستار یک مجموعه برای شما کاربر گرامی هست ولی به جهت یادگیری راحت تر این مطالب توضیحات مختصری درباره فضاهای متریک و همسایگی نقاط داده شده است.
تعاریف را با دقت مطالعه کرده و سپس برای یادگیری عمیق سایر بخش هارا بررسی کنید.
توجه: با ضربه زدن بر روی بخش مورد نظر از منوی بالا به قسمت توضیحات آن بخش بروید.
فضاهای متریک
تعریف: فرض کنید \( X \neq \emptyset \) یک مجموعه باشد. تابع \( d: X \times X \to \mathbb{R} \) یک متریک روی \( X \) نامیده میشود اگر خواص زیر را داشته باشد:
- \( d(p, q) = 0 \) اگر و تنها اگر \( p = q \)
- \( d(p, q) = d(q, p) \) برای هر \( p, q \in X \) (تقارن)
- \( d(p, r) \leq d(p, q) + d(q, r) \) برای هر \( p, q, r \in X \) (نامساوی مثلث)
- \( d(p, q) \geq 0 \) برای هر \( p, q \in X \)
در این صورت X را همراه d فضای متریک می گویند.(X ,d)
مثالها: متریکهای معروف روی \(\mathbb{R}^n\)
روی فضای \(\mathbb{R}^n\) (یعنی مجموعه همه n-تایی مرتب \((x_1, \dots, x_n)\)) متریکهای زیر قابل تعریف هستند:
- متریک اقلیدسی (فاصله اقلیدسی):
\[ d_e(u, v) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots + (x_n - y_n)^2} = \sqrt{\sum_{i=1}^n (x_i - y_i)^2} \]
که در آن \( u = (x_1, \dots, x_n) \) و \( v = (y_1, \dots, y_n) \).
- متریک منهتن (فاصله منهتن):
\[ d_1(u, v) = \sum_{i=1}^n |x_i - y_i| \]
که در آن \( u = (x_1, \dots, x_n) \) و \( v = (y_1, \dots, y_n) \).
- متریک چبیشف (فاصله چبیشف):
\[ d_m(u, v) = \max_{1 \leq i \leq n} |x_i - y_i| \]
که در آن \( u = (x_1, \dots, x_n) \) و \( v = (y_1, \dots, y_n) \).
- متریک مینکوفسکی (فاصله مینکوفسکی):
\[ d_p(u, v) = \left( \sum_{i=1}^n |x_i - y_i|^p \right)^{1/p} \]
که در آن \( u = (x_1, \dots, x_n) \) و \( v = (y_1, \dots, y_n) \).
نکته:برای \( p = 2 \) دقیقاً متریک اقلیدسی به دست میآید.
همه این توابع متریکهای معتبر روی \(\mathbb{R}^n\) هستند و فضای \(\mathbb{R}^n\) را به یک فضای متریک تبدیل میکنند.
مثال (متریک گسسته):
یکی از مهم ترین فضاهای متریک ، فضای متریک گسسته است.
فرض کنید \( X \neq \emptyset \) یک مجموعه دلخواه باشد. تابع زیر را تابع فاصله d تعریف می کنیم:
آنگاه \( d \) یک متریک روی \( X \) است و به آن متریک گسسته (یا متریک جدا) گفته میشود.
------------------------------------------------------
همسایگی یک نقطه (Neighborhood)
همسایگی یک نقطه مانند P با شعاع r مجموعه تمام نقاطی است که از نقطه p به اندازه کمتر از r فاصله دارند.
همسایگی به مرکز p ∈ X و شعاع r > 0 عبارت است از:
\(N_r(p)\) نشان دهنده همسایگی نقطه p به شعاع r است.
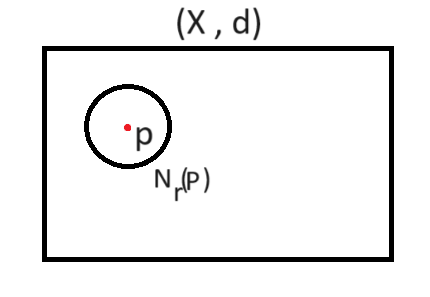
این مفهوم پایه درک نقاط درونی و بیرونی است.
نقاط درونی یک مجموعه (Interior Points)
فرض کنید (X , d) یک فضای متریک باشد ، p ∈ X , A ⊆ X.
هر نقطه را نقطه درونی A گوییم هرگاه :
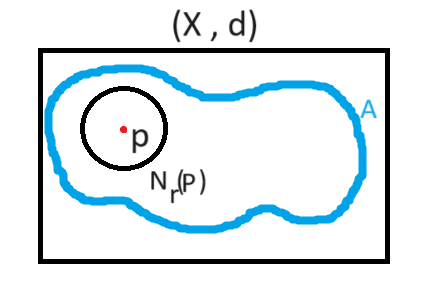
نقطه x نقطه درونی مجموعه A⊆ℝ است اگر وجود داشته باشد δ>0 بهطوری که بازه باز (p-δ, p+δ) کاملاً زیرمجموعه Aباشد.
مجموعه همه نقاط درونیA را داخلی A یا Int(A) یا °A مینامند.
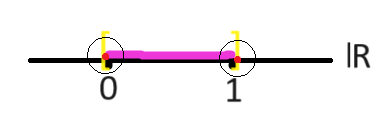
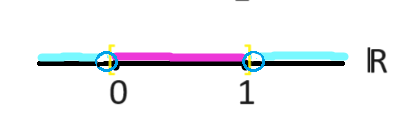
برای A = [0,1] در فضای متریک \(\mathbb{R}\)، نقاط درونی همه نقاط بازه (0,1) هستند.
نقاط ۰ و ۱ درونی نیستند، چون هر بازه بازی اطرافشان شامل نقاطی خارج از [0,1] است.
بنابراین Int([0,1]) = (0,1).
نقاط بیرونی یک مجموعه (Exterior Points)
(۲) اگر \( p \) را نقطه بیرونی \( A \) مینامیم اگر که \( p \) نقطه درونی \( A^c \) باشد. یعنی:
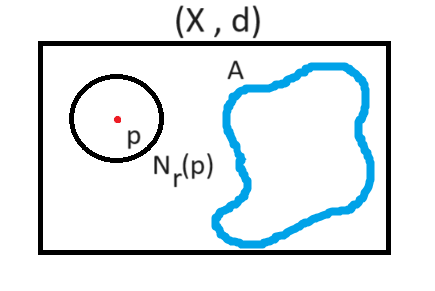
نقطه x نقطه بیرونی مجموعه A است اگر نقطه درونی متمم A (یعنی \(A^c\)) باشد. بهعبارت دیگر، وجود دارد δ>0 بهطوری که بازه باز (p-δ, p+δ) کاملاً زیرمجموعه A^c باشد.
مجموعه نقاط برونی A را با Ext(A) نمایش می دهیم.
برای A = [0,1] در فضای ℝ، نقاط بیرونی همه نقاطی هستند که یا کوچکتر از ۰ یا بزرگتر از ۱ باشند و فاصلهشان از [0,1] مثبت باشد.
مثلاً همه نقاط در (∞+,1) ∪ (0,∞-) نقاط بیرونی هستند.
نقاط مرزی (Boundary Points)
p را نقطه مرزی گویند هرگاه نه درونی نه بیرونی باشد به عبارت دیگر یعنی هر همسایگی در نقطه p باید هم A را قطع کندهم متمم A را. (P ممکن است عضو A باشد یا نباشد)یعنی:
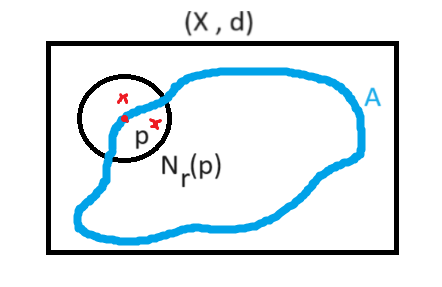
نقطه x نقطه مرزی مجموعه A است اگر هر بازه باز حاوی x هم شامل نقطهای از A و هم شامل نقطهای از A^c باشد یعنی هر چقدر هم همسایگی کوچکی اطرافش بگیریم، همیشه هم نقطهای از داخل مجموعه و هم نقطهای از خارج مجموعه در آن همسایگی وجود دارد.
مجموعه نقاط مرزی را Bd(A) یا A∂ میگویند.
برای A = (0,1)، نقاط مرزی ۰ و ۱ هستند.
برای A = [0,1] نیز نقاط مرزی همچنان ۰ و ۱ هستند.

بستار یک مجموعه (Closure)
فرض کنید \((X, d)\) یک فضای متریک و \( A \subseteq X \) باشد.
تعریف: بستار \( A \) (که با \( \overline{A} \) یا \( \operatorname{Cl}(A) \) نشان داده میشود) برابر است با اتحاد \( A \) و مجموعه نقاط مرزی آن:
\[ \overline{A} = A \cup \partial A \]
به عبارت دیگر، بستار \( A \) شامل همه نقاط خود \( A \) به علاوه همه نقاط مرزی \( A \) است.
چرا این تعریف درست است؟
- هر نقطهای که در \( A \) است، یا نقطه داخلی است یا نقطه مرزی، پس در \( A \cup \partial A \) قرار دارد.
- هر نقطه مرزی \( \partial A \) طوری است که هر توپ باز اطرافش هم به \( A \) میخورد و هم به مکمل \( A \)، بنابراین نمیتواند نقطه بیرونی باشد.
- نقاط بیرونی \( A \) (یعنی نقاطی که توپ بازی کاملاً خارج از \( A \) دارند) نه در \( A \) هستند و نه مرزی، پس در بستار نیستند.
مسائل و قضایا
مسئله: هر مجموعه زیر مجموعه بستار خود است
اثبات کنید: \( A \subseteq \overline{A} \).
فرض می کنیم \( x_0 \in A \)
چون \(d(x_0, x_0) = 0 < r \) پس \( x_0 \in N_r(x_0) \)
بنابراین \[ \forall r > 0 : \quad N_r(x_0) \cap A \neq \emptyset\]
پس\( x_0 \in \overline{A} \)
در نتیجه \( A \subseteq \overline{A} \).
قضیه:در فضای متریک گسسته، هر نقطه ، نقطه درونی هست و مرز هر مجموعه تهی است
اثبات کنید: در فضای متریک گسسته، هر نقطه ، نقطه درونی هست و مرز هر مجموعه تهی است
فرض کنید \((X, d)\) فضای متریک گسسته باشد، یعنی:
\[ d(x, y) = \begin{cases} 0 & x = y \\ 1 & x \neq y \end{cases} \]
و \( A \subseteq X \) دلخواه باشد.
قسمت اول: هر نقطه \( p \in A \) نقطه داخلی \( A \) است.
اثبات:
کافی است \( r = \frac{1}{2} \) (یا هر \( 0 < r < 1 \)) بگیریم.
حال \( N_r(p) = \{ x \in X \mid d(p, x) < r \} = \{ x \in X \mid d(p, x) < \frac{1}{2} \}\).
چون فاصلهها فقط ۰ یا ۱ هستند و \( d(p, p) = 0 < \frac{1}{2} \)، اما برای هر \( x \neq p \) داریم \( d(p, x) = 1 \not< \frac{1}{2} \)،
پس \( N_r(p) = \{p\} \subseteq A \) (زیرا \( p \in A \)).
بنابراین هر \( p \in A \) نقطه داخلی \( A \) است ⇒ \( A \subseteq \operatorname{int}(A) \subseteq A \) ⇒ \( \operatorname{int}(A) = A \). ■
قسمت دوم: مرز هر مجموعه تهی است، یعنی \( \partial A = \emptyset \).
اثبات:
فرض کنید بر خلاف، \( p \in \partial A \) وجود داشته باشد.
آنگاه \( p \) نقطه مرزی است، یعنی:
\[ \forall r > 0 : \quad N_r(p) \cap A \neq \emptyset \quad \text{و} \quad N_r(p) \cap A^c \neq \emptyset \]
حال \( r = \frac{1}{2} \) بگیریم. همانطور که بالا دیدیم:
\[ N_{\frac{1}{2}}(p) = \{p\} \]
اگر \( p \in A \)، آنگاه \( N_{\frac{1}{2}}(p) \cap A^c = \{p\} \cap A^c = \emptyset \) (تناقض).
اگر \( p \notin A \)، آنگاه \( N_{\frac{1}{2}}(p) \cap A = \{p\} \cap A = \emptyset \) (تناقض).
در هر حال تناقض به دست میآید.
بنابراین هیچ نقطه مرزی وجود ندارد ⇒ \( \partial A = \emptyset \). ■
قضیه: نقاط داخلی یک مجموعه زیرمجموعه بستار آن هستند
اثبات: نقاط داخلی یک مجموعه زیرمجموعه بستار آن هستند
فرض کنید \((X, d)\) یک فضای متریک و \( A \subseteq X \) باشد.
میدانیم (از مسئله قبلی) که همیشه \( A \subseteq \overline{A} \).
باید نشان دهیم \( \operatorname{int}(A) \subseteq \overline{A} \).
اثبات:
هر نقطه داخلی از \( A \) حتماً عضو خود \( A \) است.
یعنی اگر \( p \in \operatorname{int}(A) \)، آنگاه \( p \in A \).
بنابراین:
\[ \operatorname{int}(A) \subseteq A \]
و از فرض شناختهشده داریم:
\[ A \subseteq \overline{A} \]
پس با ترکیب این دو:
\[ \operatorname{int}(A) \subseteq A \subseteq \overline{A} \]
یعنی:
\[ \operatorname{int}(A) \subseteq \overline{A} \].■
مسئله: اگر \( A \subseteq B \)، آنگاه \( \operatorname{int}(A) \subseteq \operatorname{int}(B) \)
اثبات: اگر \( A \subseteq B \)، آنگاه \( \operatorname{int}(A) \subseteq \operatorname{int}(B) \)
فرض کنید \((X, d)\) یک فضای متریک و \( A \subseteq B \subseteq X \) باشد.
باید نشان دهیم \( \operatorname{int}(A) \subseteq \operatorname{int}(B) \).
اثبات:
فرض کنید \( p \in \operatorname{int}(A) \) دلخواه باشد.
یعنی \( p \) نقطه داخلی \( A \) است.
پس \( \exists r > 0 \) طوری که:
\[ N_r(p) \subseteq A \]
از طرفی \( A \subseteq B \)، بنابراین:
\[ N_r(p) \subseteq A \subseteq B \]
یعنی:
\[ N_r(p) \subseteq B \]
پس همان \( r > 0 \) کار میکند و \( p \) نقطه داخلی \( B \) است.
یعنی \( p \in \operatorname{int}(B) \).
چون \( p \) دلخواه در \( \operatorname{int}(A) \) بود، داریم:
\[ \operatorname{int}(A) \subseteq \operatorname{int}(B) \].■
مسئله: اگر \( A \subseteq B \)، آنگاه \( \overline{A} \subseteq \overline{B} \)
اثبات: اگر \( A \subseteq B \)، آنگاه \( \overline{A} \subseteq \overline{B} \)
روش اول (مستقیم از تعریف بستار):
فرض کنید \( p \in \overline{A} \) دلخواه باشد.
یعنی برای هر همسایگی دلخواه با شعاع \( r > 0 \):
\[ N_r(p) \cap A \neq \emptyset \]
بنا به فرض \( A \subseteq B \)، پس:
\[ N_r(p) \cap A \subseteq N_r(p) \cap B \]
بنابراین \( N_r(p) \cap B \neq \emptyset \).
این برای هر \( r > 0 \) دلخواه برقرار است، پس \( p \in \overline{B} \).
چون \( p \) دلخواه بود، \( \overline{A} \subseteq \overline{B} \). ■
روش دوم (با استفاده از مکمل و قضیه داخلی):
فرض \( A \subseteq B \).
آنگاه \( B^c \subseteq A^c \).
⇒ \( (B^c)^\circ \subseteq (A^c)^\circ \)
⇒ \( (\overline{B})^c \subseteq (\overline{A})^c \)
⇒ \( \overline{A} \subseteq \overline{B} \). ■